最长回文子串

5. 最长回文子串 - 力扣（LeetCode）

题目描述

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

题解一：暴力求解

两层循环，第一层循环作为判断的起点，第二层循环作为判断的终点，每次都判断是否是回文子串，并且根据长度来更新result，但是时间复杂度相当高！（这个题解可能是正确的，因为超时了，我不知道所有样例是否结果正确，但是前90个正确:grinning:）

class Solution {
public:
    bool huiwen(vector<char> s) {
        for (int i = 0; i < s.size() / 2; i++) {
            if (s[i] != s[s.size() - i - 1])
                return false;
        }
        return true;
    }
    string longestPalindrome(string s) {
        vector<char> s1;
        int flag = 0;
        int a = INT_MIN;
        string result;
        for (int i = 0; i < s.size() - 1; i++) {
            s1.push_back(s[i]);
            for (int j = i + 1; j < s.size(); j++) {
                s1.push_back(s[j]);
                if (huiwen(s1)) {
                    flag++;
                    if (j - i > a) {
                        a = j - i;
                        result = string(s1.begin(), s1.end());
                    }
                }
            }
            s1.clear();
        }
        if (flag > 0)
            return result;
        result = s[0];
        return result;
    }
};

题解二：动态规划

什么是动态规划？

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

在本问题中

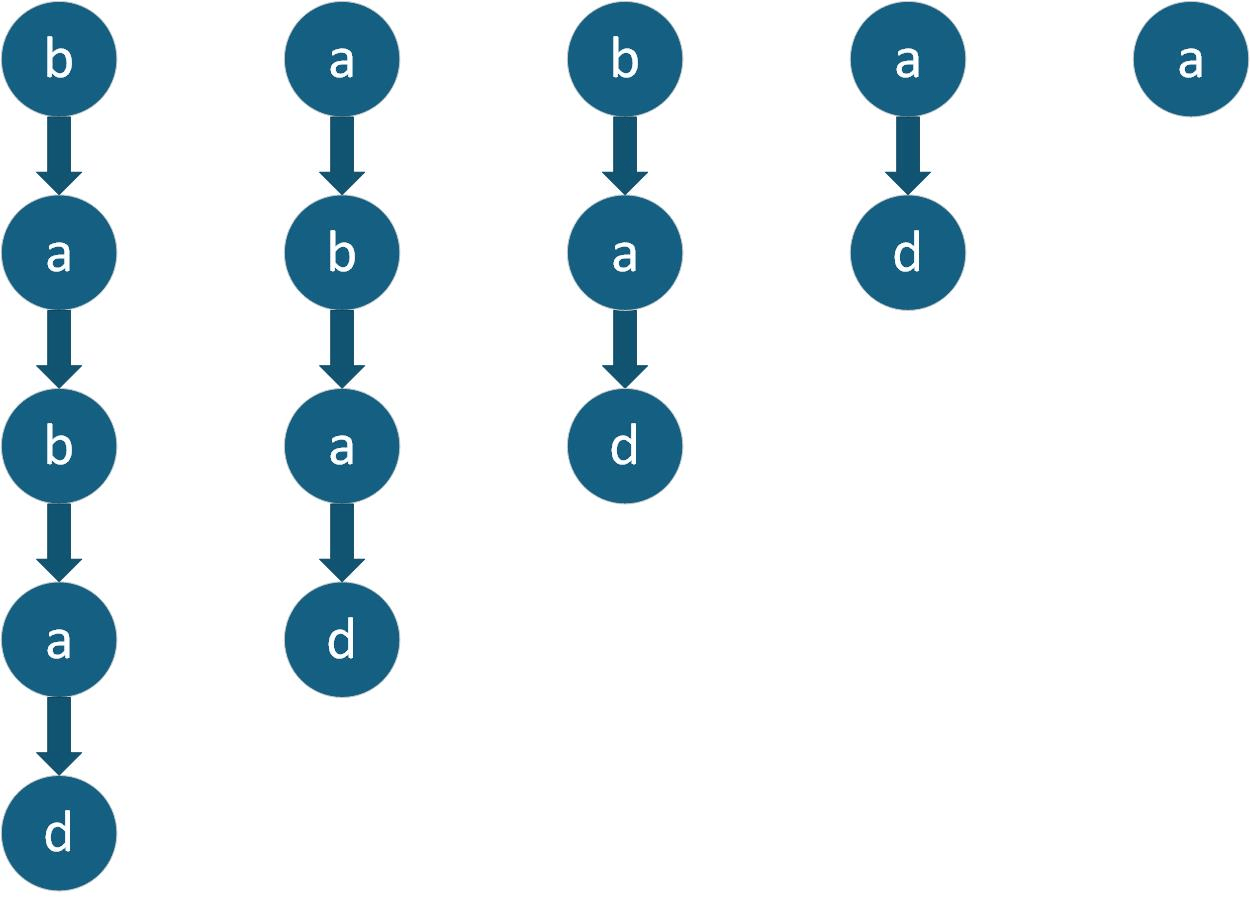
可以看到，有大量的重复操作，那么这就符合dp操作的要求。

接下来看具体操作。

动态规划dp数组的确定，并确定初始化dp数组的值

vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
for (i = 0; i < s.size(); i++) {
            dp[i][i] = true;  //初始化，单个字符永远都是回文子串
        }

确定递推公式

如果s[i] != s[j]，那么dp[i][j]肯定是false

如果s[i] == s[j]，那么dp[i][j]的值有以下几种情况

1. 长度为1，肯定是回文子串

2. 长度为2，如aa，肯定是回文子串

3. 长度大于2，回文子串取决于内部的子串（掐头去尾）。例如abba，因为bb是回文子串，所以abba也是；又例如abca，因为bc不是，所以abca不是。

if (s[i] != s[j]) {  //不是回文子串
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {  //长度小于3，直接标记为true
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];  //长度大于等于3，取决于中间是否为true
                    }
                }

确定遍历顺序
根据递推公式，我们知道，在某些情况下，如果想要知道dp[i][j]，就必须要知道dp[i+1][j-1]的值

下面我们看一下初始化后的矩阵(babad)

遍历完成后

4.最终代码

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() < 2)
            return s;
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        int i, j;
        int max_len = 1;
        int start = 0;
        for (i = 0; i < s.size(); i++) {
            dp[i][i] = true;
        }

        for (i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] != s[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i + 1 < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }
                if (dp[i][j] && j - i + 1 > max_len) {
                    max_len = j - i + 1;
                    start = i;
                }
            }
        }

        return s.substr(start, max_len);
    }
};

关于动态规划的相关资料看一遍就理解：动态规划详解 - 知乎